If any people reading these short notes are competent in mathematics, physics, statistics, ecology, biology or management theory, I beg their pardon for the childish simplification of the reasoning and the pictures. I am not trying to offer scientifically strict or philosophically accurate models or patterns, but only a few hints for practical thinking.
I am not trying to get into the elaborate analyses of the Chaos Theory, turbulent systems and complexity. There is abundant literature on these subjects – and for many years it has been clear (at least in theory) that it doesn’t concern only physics, meteorology or engineering, but also human behavior – and, therefore, organizations, society, the economy, politics and culture.
Let’s begin with an observation that may appear simplistic. But “obvious” facts are often a good starting point.
When we are planning to go from A to B, the concept appears in our mind as a straight line:
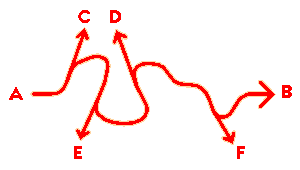
In a real world there are no straight lines. Between A and B there are obstacles, interferences, indirect routes, so that even if the task is extremely simple, such as going out for a cup of coffee, our actual behavior is likely to take this sort of shape:
In a task as simple as this, that takes a few minutes, it’s unlikely that in the meantime we shall forget where we are going and why.
But the problem takes a different shape when it involves an organization, with much greater complexities, unexpected events, constant change of the situation and the environment, etcetera.
Any group of people doing something together is, de facto, an organization. Even four or five people meeting for a cup of coffee. And even in the simplest case reality is more complex than is shown in these flat pictures. Going to the coffee house involves a three-dimensional route, because there are probably stairs or elevators. In an organization, even when it’s small, the model is obviously multi-dimensional. The “flat” diagrams that I am using to summarize the picture are necessarily less complex that the situation in actual experience. But I hope simplification can help to understand the basic nature of the problems, that would be hard to detect in an analytical “topology”.
So it becomes possible (it actually happens quite often) that some parts of the organization forget the original direction...
... and the entire system loses sight of the objective, with the added complication that several people or groups think that they are heading for C, D, E or F and therefore they work in disharmony with each other and with the organization as a whole. This is, in any case, a serious problem – but it’s to be noted that people heading for C or F are shifting, though on a lateral course, toward B, while those heading for D or E are moving in the opposite direction – and in order to return to a route leading to B they will need a complex, cumbersome (and often expensive) detour. It’s quite easy, observing the behavior of organizations, to notice how often this sort of thing is happening.
In an environment that isn’t changing, or where evolution is predictable and controllable, there is (if only in theory) a simple solution. Everybody should have a compass. That is to say, nobody should be left to carry out a task without understanding a broader perspective. All parts of the organization should know that the objective is B, and the process should be continually monitored so that the (unavoidable) deviations return as soon as possible to the right direction. The system, therefore, would behave like this:
But in a complex and turbulent environment the process could evolve quite differently. The situation is mutating and unpredictable. Heading only toward objective B may turn out to be a mistake.
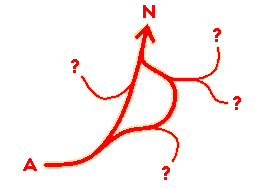
If we look back a the third picture, with diverging directions, we notice that (for instance) two “spontaneous” deviations (C and D) are converging in an unforeseen direction. It may be useful to find out why. We could discover that this is the situation:
In this example the “turbulent” evolution of the system has led us to discover a new objective N – and to understand that it’s convenient to concentrate our energies in that direction, while not losing sight of other “branches” that could reveal unexpected opportunities.
We notice that some of those “branches” have directions relatively close to our “old” objective B, some don’t move far away from our “new” objective N, while others point to still unexplored territories – and that the entire system has taken a shape that may be less “logical”, but is structurally more simple than those generated by forcing the system to follow a “linear” model.
The fact is that “complexity” (or “chaos”) isn’t inherently more complex than apparently “orderly” systems – and it can lead to simplicity. The problem is that we are not trained to understand how it works.
This looks more like the growth of a climbing tree than the structure of a machine or the manufacturing of an industrial product. Quite often the study of complexity leads to biological analogy.
It could be quite complicated to study the theoretical implications of this (pretty obvious) conclusion. But a simple, intuitive perception of this fact can help us to understand how to behave in a world dominated by turbulence and complexity, where “non linear” thinking is often the winner.